[Review] Concept Embedding Models: Beyond Accuracy-Explainability Trade-off

Abstract

• Publication: NeurIPS 2022
• Citation: 54(24.08.13)
• 주제: Concept Bottleneck Model(CBM)에서 concept을 임베딩으로 표현
• 연구 배경
  • CBM은 concept을 scalar로 표현
  • Real-world에는 너무 많은 concept 존재
  • Language Model에서 모든 단어를 정수값으로 표현하지 않듯이, concept로 embedding으로 표현
• 문제: concept을 고차원 임베딩으로 표현했기때문에 explain이 어려워짐

Background

Concept Bottleneck Model(CBM)

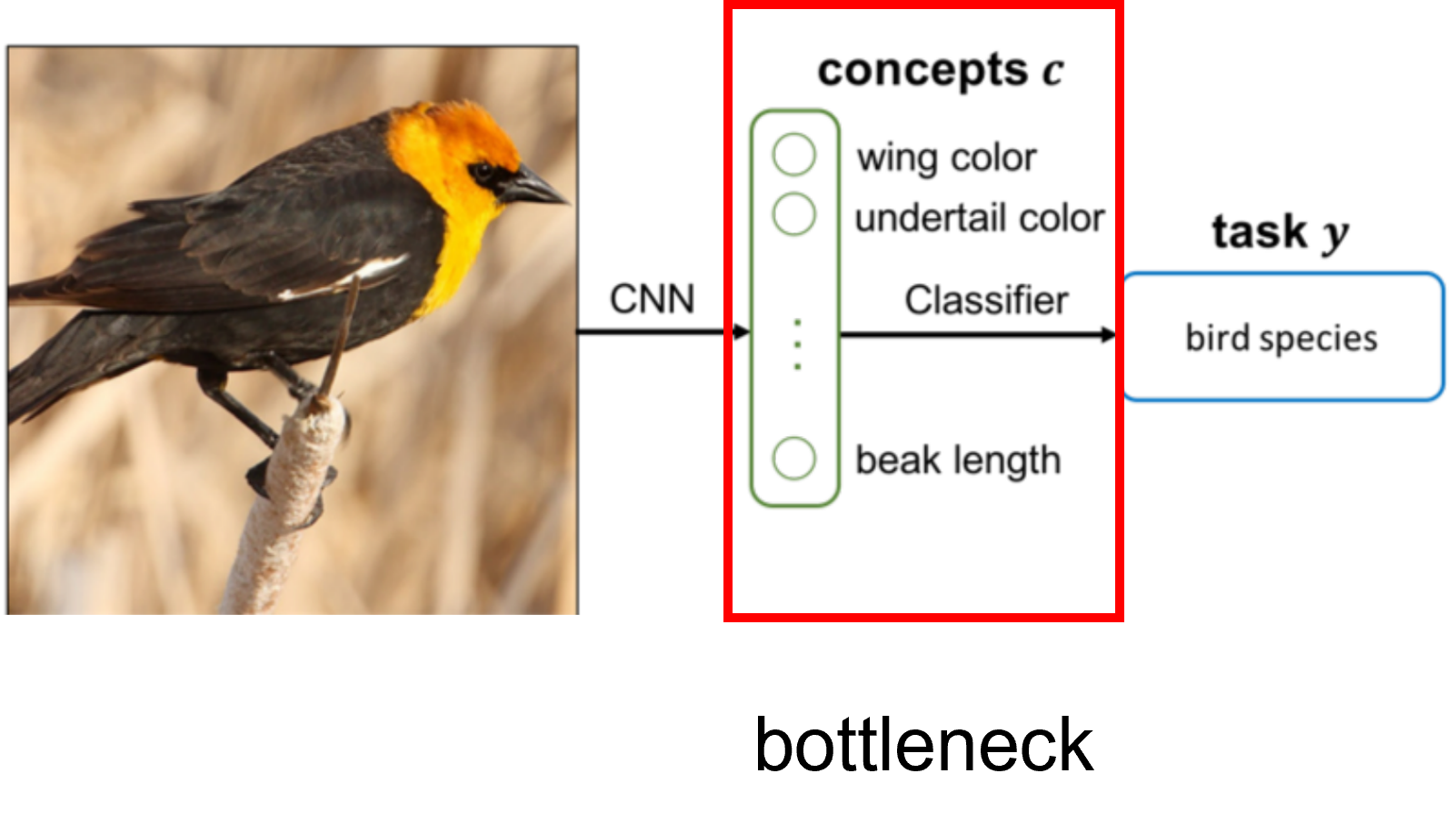
CBM을 개념적으로만 설명하겠다. CBM은 사람이 지정한 concept을 학습하고, 그것을 이용해 task를 수행하는 새로운 모델이다. 이 모델은 두 가지의 중요한 기능이 있다. 첫 번째는 학습한 concept으로 분류, 회귀 문제를 품으로써 모델의 예측에 설명성을 부여했다는 것이다. 두 번째는 추론 시간에 전문가가 개입하여 모델이 잘못 예측한 concept을 수정함으로써 최종 출력을 옳게 고칠 수 있다는 것이다.

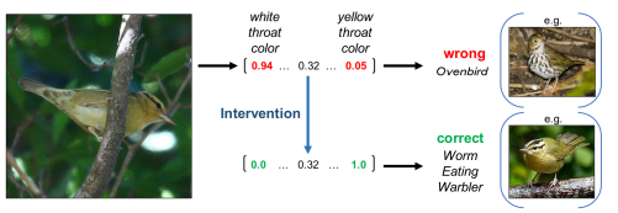
하지만 CBM은 concept을 scalar로 표현하기 때문에 다양한 concept을 표현하기 어렵고 학습 단계에서 보지 못한 concept을 마주할 때 성능이 떨어진다. 본 논문은 CBM의 concept을 임베딩으로 표현함으로써 위 문제를 해결한다.

Concept Embedding Model(CEM)

Architecture

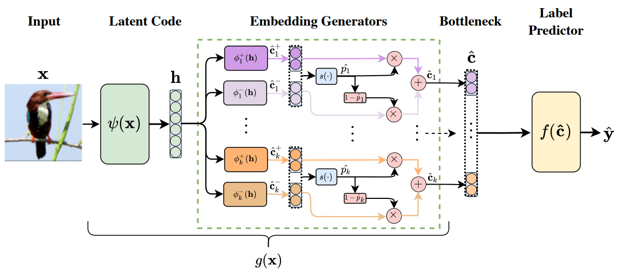
Latent Code

입력 이미지 x를 DNN인 $\psi(\cdot)$에 입력해 $h\in R^m$을 얻는다.

Embedding Generators

Embedding Generators는 $h$를 $\phi(\cdot)$을 이용해 사용자가 설정한 k개의 concept $c_i$를 임베딩으로 표현한다. 각 concept은 $c_i$가 입력 x에 존재하는지를 나타내는 $\hat{c}^+$와 $\hat{c}^-$로 표현된다. $c$를 $\hat{c}^+$와 $\hat{c}^-$로 나누는 이유는 concept intervention을 위함이기 때문에 아래에서 설명한다. $\hat{c}^+$와 $\hat{c}^-$로 나눈 concept은 $\hat{p_i}$를 이용해 $\hat{c}^+$와 $\hat{c}^-$의 가중합으로 합친다. \(\hat{c}_i = \hat{p}\times \hat{c}^++(1-\hat{p})\times\hat{c}^- ,\\ where\ \hat{p}=\sigma(W[\hat{c}^+, \hat{c}^-]^T+b_s)\) 그림 상으로도 보이다시피 h가 FC 레이어를 거쳐 얻은 $\hat{c}(\hat{c}=\phi(h))$와 Bottleneck에 들어간 concept이 같은 형태이다. $\hat{c}$에 단순히 스칼라인 p를 곱하고 더하는 연산밖에 없기 때문에 차원이 변하지 않는다. 따라서 위 수식을 거치지 않고 곧바로 $\hat{c}$을 사용해도 될 것 같지만 굳이 복잡한 과정을 거치는 이유는 concept 학습과 explainability 때문인것 같다.

CEM의 학습 loss는 아래와 같다. \(L_{task}(y,f(h)) + \alpha L_{CrossEntopy}(c,\hat{p}(x)), where\\ c=[c_1, ...,c_k]\\ \hat{p}(x)=[\hat{p}_1,...,\hat{p}_k]\) 사용자가 제공하는 concept $c_i$는 해당 개념이 존재여부에 해당하는 scalar이므로 $c$는 k개의 원소로 이루어진 벡터이다. $c\in R^k$인 $c$와의 cross entopy 함수를 적용하기 위해서는 $\hat{p(x)}$ 역시 $\hat{p(x)}\in R^k$이어야 한다. CEM으로 넘어오며 concept을 임베딩 벡터로 표현하면서 예측한 concept값도 고차원 임베딩이 되면서 concept을 학습하기 위해 사용하던 cross entopy loss를 사용할 수 없어져 새로운 concept 값이 필요해 위와 같은 과정을 거치게 된 것으로 보인다. 이를 통해 concept에 임베딩 벡터를 도입함으로써 성능을 향상시키고, 그에 따른 trade-off인 설명성이 하락하는 문제를 $p$로 해결한다.

Bottleneck

$\hat{c} = [\hat{c}_1,…,\hat{c}_k]$

Label Predictor

$\hat{y}=f(\hat{c})$로 label 예측한다. $f(\cdot)$은 MLP이다.

Concept Intervention

위에서 언급한 $\hat{p}$를 이용해 잘못된 $\hat{c}$를 바로잡는다. \(\hat{c}=\hat{p}\times \hat{c}^+ + (1-\hat{p})\times \hat{c}^- \\ if)\ \hat{p}=0, \hat{c} = \hat{c}^- \\ if ) \ \hat{p}=1, \hat{c}=\hat{c}^+\) $\hat{p}$가 0이면 false concept embedding을 취하고, $\hat{p}$가 1이면 true concept embedding을 취하게 되어 concept intervention이 가능하다. 또한, 여기서 $\hat{c}$를 $\hat{c}^+$와 $\hat{c}^-$로 나누어 표현한 이유가 드러난다. positive와 negative 구분해서 표현해야 $\hat{p}$에 따라 intervention이 더 효과적으로 이루어지기 때문이다.