백준 2579번 (cpp)

계단오르기

---

시작점부터 도착점까지 계단을 오르면서 최대의 점수를 얻는 문제

규칙

• 3계단 연속은 안됨
• 한번에 한칸이나 두칸만 오를수있음
  

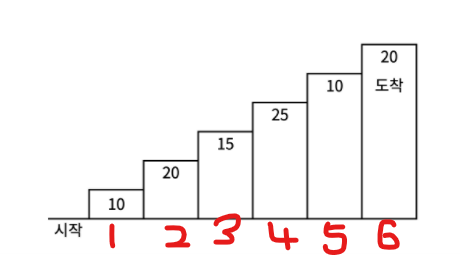
풀이 개념

6번까지 도착했을때의 최댓값을 구하기 위해서는 5번까지 최댓값을 구하고 6번을 밟으면 된다.
그럼 5번의 최댓값은 4번의 최댓값에서 5번을 밟는거.

1. 공중제비를 하면서 봐도 최적 부분 구조를 갖는다고 볼수있다.
2. 각 계단의 최댓값을 중복적으로 사용한다.

동적계획법을 사용하면 좋다.

풀이 방법

계단을 오르는데 3계단 연속 밟는게 불가능한 것을 유의해야한다. 만약 i번째 계단의 최댓값을 구하고 싶다면 다음과같이 두가지 경우중 하나를 고를수 있다.

• i-3밟고 i-2밟고 i밟기
• i-2밟고 i밟기

위의 1번과 2번중 더 큰값을 고른다면 항상 규칙을 지킬수 있다.
3번째 계단부터 i번째 계단까지 반복문을 돌리며 최댓값을 구했을 경우 규칙에 위배되지 않으며 모든 경우의 수를 탐색해 최댓값을 구할 수 있다.

코드

#include<iostream>
using namespace std;
int main(){
    int N;
    cin>>N;
    int steps[N+1]; //숫자와 인덱스를 동일하게 매칭하기 위해 N+1만큼 할당
    for(int i=1; i<=N; i++){
        cin>>steps[i];
    }
    int dp[N+1];
    dp[0] = 0;
    dp[1] = steps[1];   
    dp[2] = steps[1] + steps[2];    //초기 세팅
    for(int i=3; i<=N; i++){
        dp[i] = max(dp[i-3]+steps[i-1]+steps[i],dp[i-2]+steps[i]);
    }
    cout<<dp[N];
    return 0;
}